STEP4:説明変数が1つになるまで繰り返す
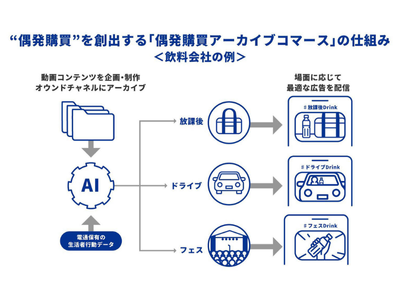
今度は、「面積」を除いた「接客」「品揃え」「立地」の3つの変数で回帰分析をかけます。
3つの変数の場合、出力結果は以下のとおりです。
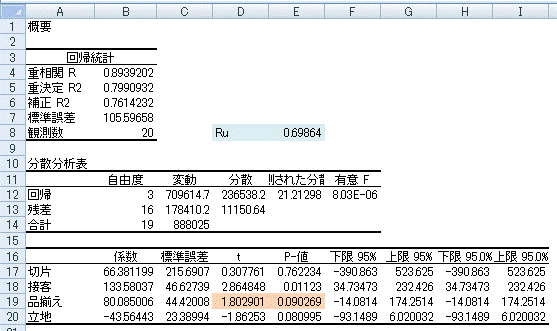
Ruの計算は、前回入力した数式を同じセル(ここでは、E8)にコピーすれば、計算式を一から入力しなくても自動的に計算してくれます。
3つの説明変数の中では、今度は|1.803|の「品揃え」のtの絶対値が一番小さいので、「品揃え」を削除して、「接客」「立地」で回帰分析を行います。以上のように、説明変数が最後の1つになるまで、回帰分析をかけ、その時のRu値を求めます。
STEP5:すべての結果のRuを比較し、最大になる組み合わせを探す
4回の変数選択パターンとそれぞれの回帰分析結果を表にまとめてみました。精度を測る指標を比較できるように、重相関R、補正R2、そして今回変数選択規準に採用したRuをそれぞれ抜粋しています。
表の見方は、No1は、説明変数を4つすべて採用した時の、重相関R、補正R2、そしてRuの数値です。見るべき項目は、変数選択基準のRuですが、参考までに重相関R、補正R2の値も載せています。重相関Rが精度を測る指標として使えない理由は後述します。

Ruの値が大きいのは、2回目の「接客」「品揃え」「立地」の3つの説明変数の場合であり、この組み合わせが、より精度の高い重回帰式であることを示しています。
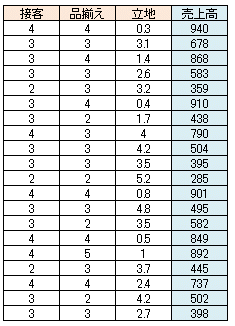
変数が3つの時の出力結果は、以下の通りです。
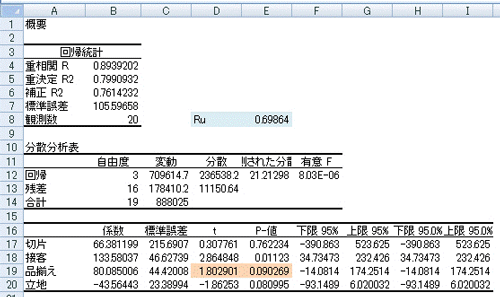
よって、最適な回帰モデルは、以下となります。
改めて、このモデルで、新しく予定している初台店の売り上げを予測してみます。

売上高=66.38+133.58×4+80.09×4-43.56×立地
=899.26(千円)
補足:重相関Rと重決定R2が変数選択規準として使えない理由
[回帰分析]をかけた時に出力される結果のうち、重相関Rと重決定R2は、式の都合上、説明変数が目的変数に影響しているかどうかに関係なく、説明変数の数を増えるほど1に近づいていくという性質があります。以下の表とグラフは、説明変数を増やしていった時の各指標の変化を表したものです。
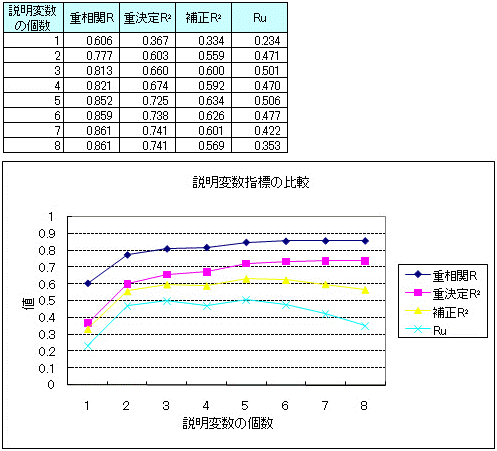
よって、重相関Rと重決定R2がどの変数の組み合わせが一番効果的かということを決める説明変数選択規準としては適切ではありません。
そこで、説明変数の数による影響を排除した指標が、補正R2や上田の説明変数選択規準Ruになります。今回は、Ruを使いましたが、補正R2(正確には、自由度調整済寄与率)を利用しても構いません。補正R2もRuもほぼ同一の結果になりますが、場合によって(特にデータ数が少ない時)、補正R2の方がより多く説明変数を採用する傾向があります。
次回は、重回帰分析の仕上げとして、説明変数に相関の高いものを取り込んだ時のリスク (=多重共線性(マルチコ))の問題を解説します。